Abstract
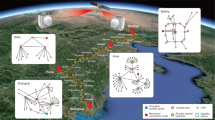
A quantum network1,2,3 provides an infrastructure that connects quantum devices with revolutionary computing, sensing and communication capabilities. A quantum satellite constellation offers a solution to facilitate the quantum network on a global scale4,5. The Micius satellite has verified the feasibility of satellite quantum communications6,7,8,9; however, scaling up quantum satellite constellations is challenging, requiring small lightweight satellites, portable ground stations and real-time secure key exchange. Here we tackle these challenges and report the development of a quantum microsatellite capable of performing space-to-ground quantum key distribution using portable ground stations. The microsatellite payload weighs approximately 23 kilograms, and the portable ground station weighs about 100 kilograms, representing reductions by more than 1 and 2 orders of magnitude, respectively. Using this set-up, we demonstrate satellite-based quantum key distribution with multiple ground stations and achieve the sharing of up to 1.07 million bits of secure keys during a single satellite pass. In addition, we multiplex bidirectional satellite–ground optical communication with quantum communication, enabling key distillation and secure communication in real time. Also, a secret key, enabling one-time pad encryption of images, is created between China and South Africa at locations separated by over 12,900 kilometres on Earth. The compact quantum payload can be readily assembled on existing space stations10,11 or small satellites12, paving the way for a satellite-constellation-based quantum and classical network for widespread real-life applications.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available at Zenodo at https://doi.org/10.5281/zenodo.14732295 (ref. 61).
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Azuma, K. et al. Quantum repeaters: from quantum networks to the quantum internet. Rev. Mod. Phys. 95, 045006 (2023).
Lu, C.-Y., Cao, Y., Peng, C.-Z. & Pan, J.-W. Micius quantum experiments in space. Rev. Mod. Phys. 94, 035001 (2022).
Bedington, R., Arrazola, J. M. & Ling, A. Progress in satellite quantum key distribution. npj Quantum Inf. 3, 30 (2017).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Yin, J. et al. Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140–1144 (2017).
Ren, J.-G et al. Ground-to-satellite quantum teleportation. Nature 549, 70–73 (2017).
Liao, S.-K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
International space station. NASA https://www.nasa.gov/international-space-station/ (2025).
Gu, Y. The China space station: a new opportunity for space science. Natl Sci. Rev. 9, nwab219 (2022).
Albulet, M. Spacex Non-geostationary Satellite System: Attachment A Technical Information to Supplement Schedules (US Federal Communications Commission, 2016).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In International Conference on Computer System and Signal Processing 175–179 (IEEE, 1984).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661 (1991).
Xu, F., Ma, X., Zhang, Q., Lo, H.-K. & Pan, J.-W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 92, 025002 (2020).
Peng, C.-Z. et al. Experimental long-distance decoy-state quantum key distribution based on polarization encoding. Phys. Rev. Lett. 98, 010505 (2007).
Rosenberg, D. et al. Long-distance decoy-state quantum key distribution in optical fiber. Phys. Rev. Lett. 98, 010503 (2007).
Liu, Y. et al. Experimental twin-field quantum key distribution over 1000 km fiber distance. Phys. Rev. Lett. 130, 210801 (2023).
Bennett, C. H. & Brassard, G. Experimental quantum cryptography: the dawn of a new era for quantum cryptography: the experimental prototype is working. ACM SIGACT News 20, 78–80 (1989).
Peng, C.-Z. et al. Experimental free-space distribution of entangled photon pairs over 13 km: towards satellite-based global quantum communication. Phys. Rev. Lett. 94, 150501 (2005).
Schmitt-Manderbach, T. et al. Experimental demonstration of free-space decoy-state quantum key distribution over 144 km. Phys. Rev. Lett. 98, 010504 (2007).
Sidhu, J. S. et al. Advances in space quantum communications. IET Quantum Commun. 2, 182–217 (2021).
de Forges de Parny, L. et al. Satellite-based quantum information networks: use cases, architecture, and roadmap. Commun. Phys. 6, 12 (2023).
Chen, Y.-A. et al. An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature 589, 214–219 (2021).
Liao, S.-K. et al. Space-to-Ground quantum key distribution using a small-sized payload on Tiangong-2 space lab. Chin. Phys. Lett. 34, 090302 (2017).
Oi, D. K. et al. CubeSat quantum communications mission. EPJ Quantum Technol. 4, 6 (2017).
Neumann, S. P. et al. Q3Sat: quantum communications uplink to a 3U CubeSat-feasibility & design. EPJ Quantum Technol. 5, 4 (2018).
Kerstel, E. et al. Nanobob: a CubeSat mission concept for quantum communication experiments in an uplink configuration. EPJ Quantum Technol. 5, 6 (2018).
Haber, R., Garbe, D., Schilling, K. and Rosenfeld, W. QUBE – a cubesat for quantum key distribution experiments. In Proc. 32nd Annual AIAA/USU Conference on Small Satellites, SSC18-III-05 (Utah State University, 2018).
Podmore, H. et al. Optical terminal for Canada’s Quantum Encryption and Science Satellite (QEYSSat). In Proc. 2019 IEEE International Conference on Space Optical Systems and Applications 1–5 (IEEE, 2019).
Miller, A. V. et al. Vector-towards quantum key distribution with small satellites. EPJ Quantum Technol. 10, 52 (2023).
Ahmadi, N. et al. QUICK 3 design of a satellite based quantum light source for quantum communication and extended physical theory tests in space. Adv. Quantum Technol. 2300343, 1–9 (2024).
Villar, A. et al. Entanglement demonstration on board a nano-satellite. Optica 7, 734 (2020).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Tomamichel, M., Lim, C. C. W., Gisin, N. & Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 3, 634 (2012).
Lim, C. C. W., Curty, M., Walenta, N., Xu, F. & Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307 (2014).
Roberts, G. L. et al. Patterning-effect mitigating intensity modulator for secure decoy-state quantum key distribution. Opt. Lett. 43, 5110 (2018).
Agnesi, C., Avesani, M., Stanco, A., Villoresi, P. & Vallone, G. All-fiber self-compensating polarization encoder for quantum key distribution. Opt. Lett. 44, 2398 (2019).
Li, Y. et al. High-speed robust polarization modulation for quantum key distribution. Opt. Lett. 44, 5262 (2019).
Wang, X.-B., Peng, C.-Z., Zhang, J., Yang, L. & Pan, J.-W. General theory of decoy-state quantum cryptography with source errors. Phys. Rev. A 77, 042311 (2008).
Paraïso, T. K. et al. A photonic integrated quantum secure communication system. Nat. Photon. 15, 850–856 (2021).
Liao, S.-K. et al. Long-distance free-space quantum key distribution in daylight towards inter-satellite communication. Nat. Photon. 11, 509–513 (2017).
Li, Y. et al. Space-ground QKD network based on a compact payload and medium-inclination orbit. Optica 9, 933 (2022).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters. Nature 557, 400–403 (2018).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Luo, W.-B. et al. Research on polarization compensation for practical satellite-based quantum key distribution. Opt. Commun. 570, 130925 (2024).
Zhang, L. et al. Design and in-orbit test of a high accuracy pointing method in satellite-to-ground quantum communication. Opt. Express 28, 8291–8307 (2020).
Qian, Y. et al. Note: A 10 gbps real-time post-processing free physical random number generator chip. Rev. Sci. Instrum. 88, 096105 (2017).
Herrero-Collantes, M. & Garcia-Escartin, J. C. Quantum random number generators. Rev. Mod. Phys. 89, 015004 (2017).
Jiang, C., Yu, Z.-W. & Wang, X.-B. Measurement-device-independent quantum key distribution with source state errors and statistical fluctuation. Phys. Rev. A 95, 032325 (2017).
Chau, H. F. Decoy-state quantum key distribution with more than three types of photon intensity pulses. Phys. Rev. A 97, 040301 (2018).
Tomamichel, M. & Renner, R. Uncertainty relation for smooth entropies. Phys. Rev. Lett. 106, 110506 (2011).
Currás-Lorenzo, G. et al. Tight finite-key security for twin-field quantum key distribution. npj Quantum Inf. 7, 22 (2021).
Jiang, C., Hu, X.-L., Yu, Z.-W. & Wang, X.-B. Composable security for practical quantum key distribution with two way classical communication. New J. Phys. 23, 063038 (2021).
Lo, H.-K., Chau, H. F. & Ardehali, M. Efficient quantum key distribution scheme and a proof of its unconditional security. J. Cryptol. 18, 133–165 (2005).
Sidhu, J. S., Brougham, T., McArthur, D., Pousa, R. G. & Oi, D. K. Finite key performance of satellite quantum key distribution under practical constraints. Commun. Phys. 6, 210 (2023).
Liao, S.-K. Data for ‘microsatellite-based real-time quantum key distribution’. Zenodo https://doi.org/10.5281/zenodo.14732295 (2025).
Acknowledgements
We thank W.-S. Tang, C.-W. Feng, J.-S. Dai, T.-T. Wang, T. Tang, Y.-C. Ji, S.-Q. Fan and Z. Wang for their efforts in the development of the payloads and the microsatellite; H.-B. Li, Z. Wang, W.-W. Ye, S.-J. Xu, X. Li, X. Han, Z.-G. Xiao, L.-K. Guo, C.-F Zhu and Y.-Y. Wang for their long-term assistance in observations and experimental measurements; Q.-Y. Yao, S.-Q. Zhao and Y.-G. Zhao for their efforts in the development of the portable OGSs; and Z.-Y. Chen, C.-L. Li and L.-Y. Han for discussions. This work was supported by National Natural Science Foundation of China (92476203, T2125010, 61961146002, 12174374, 92476001, 12374475 and 62031024), National Key Research and Development Program of China (2020YFA0309701 and 2018YFE0200600), Key R&D Plan of Shandong Province (2021ZDPT01), Jinan Innovation Zone, Innovation Program for Quantum Science and Technology (2021ZD0300104, 2021ZD0300108 and 2021ZD0300300) and Shanghai Municipal Science and Technology Major Project (2019SHZDZX01).
Author information
Authors and Affiliations
Contributions
C.-Z.P. and J.-W.P. conceived the research. S.-K.L., C.-Z.P. and J.-W.P. designed the experiment. Y.L., S.-K.L., Y.-H.L, J.Y. and C.-Z.P. developed the compact QKD light source. L.Z., H.-Y.W., J.-C.W., T.C., S.-K.L. and C.-Z.P. developed the satellite tracking technique. M.Y., C.-Z.W., Y.L., W.-Q.C., S.-K.L. and C.-Z.P. developed the multiplexed quantum and classical communication. S.-K.L., Y.L., W.-Q.C., C.-Z.W., M.Y., L.Z., H.-Y.W., L.C., J.-C.W., X.-Y.T., T.C., C.-F.L., J.Z., F.-Z.L., W.-Y.L., J.Y., R.S., C.-Z.P., J.-Y.W. and J.-W.P. developed the satellite and payloads. J.-G.R., B.J., H.-J.X., X.-J.L., H.L., G.-W.Y., H.-L.Y., Y.C., J.Y., S.-K.L., C.-Z.P. and J.-W.P. developed the portable OGSs. X.-B.W., C.J. and C.-Z.W. contributed to the decoy-state analysis. S.-K.L., Y.L., J.-G.R., B.J., H.-L.Y., W.-Q.C., C.-Z.W., M.Y., L.Z., H.-Y.W., C.W., F.-Z.L., W.-B.L., Y.I., F.P., H.-Z.C., X.-H.T., S.-J.X., F.Z., N.-L.L., L.L., Y.C., J.Y., Q.Z., C.-Z.P. and J.-W.P. contributed to the experiment such as data collection. Y.L., S.-K.L., F.X., Q.Z., C.-Z.P. and J.-W.P. analysed the data and wrote the paper, with input from C.-Z.W., M.Y., L.Z., B.J., H.-L.Y. and C.J. J.-W.P. supervised the whole project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Schematic of the polarization compensation process on the Poincaré sphere.
a, The first QWP moves the corresponding point \({R}^{{\prime} }\) to the equatorial plane, where the corresponding points \({D}^{{\prime} }\) and \({H}^{{\prime} }\) will appear on a warp coil. The central axis for rotation is the projection axis of \(o{R}^{{\prime} }\) (o is the original point) on the equatorial plane. b, The second QWP moves the corresponding point \({H}^{{\prime} }\) to the equatorial plane, where the corresponding point \({R}^{{\prime} }\) will be in the pole position. The central axis for rotation is the projection axis of \(o{H}^{{\prime} }\) on the equatorial plane. c, The HWP moves the corresponding point \({H}^{{\prime} }\) to the original position of point H. The central axis for rotation is the middle axis of \(o{H}^{{\prime} }\) and oH. d, The corresponding points \({R}^{{\prime} }\), \({H}^{{\prime} }\) and \({D}^{{\prime} }\) will return to their original positions of R, H and D (\({R}^{{\prime} }\) coincides with R, \({H}^{{\prime} }\) coincides with H, \({D}^{{\prime} }\) coincides with D. The three wave plates help realize the previous unitary transformation process \({U}^{{\prime} }\).
Extended Data Fig. 2 QBER contribution of noise and satellite elevation angle as functions of time.
The transmitted vacuum state allows for the assessment of the polarization-independent QBER arising from factors such as background noise. In urban environments, background noise is a dominant contributor to the QBER, particularly at low satellite elevation angles where received photon counts are reduced. This impact varies depending on ground station location, time of day, and weather conditions. Employing spectral filtering with narrower linewidth and spatial filtering with smaller field of view can further mitigate this issue.
Extended Data Fig. 3 Method of satellite attitude control.
We incorporate the detected uplink beacon laser of the capture camera into the closed loop of satellite attitude control to achieve precise satellite attitude control.
Extended Data Fig. 4 Laser communication principles.
a, Hardware schematic for laser communication. b, Implementation of time synchronization using laser communication. FPGA, field programmable gate array; CDR, clock and data recovery; EDFA, erbium-doped fiber amplifier.
Extended Data Fig. 5 Procedure of laser-communication-based time synchronization and key distillation.
RND, random number; TDC, time-to-digital converter; LDPC, low-density parity check; CRC, cyclic redundancy check.
Extended Data Fig. 6 Illustration of the processes of key relay and encrypted communication between Jinan station and Nanshan station within two satellite orbits.
a, Key relay. b, Encrypted communication. By leveraging the satellite as a trusted relay, both key relay and encrypted communication can be realized between the two OGSs.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, Y., Cai, WQ., Ren, JG. et al. Microsatellite-based real-time quantum key distribution. Nature 640, 47–54 (2025). https://doi.org/10.1038/s41586-025-08739-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-025-08739-z